車載毫米波雷達的設計的諸多挑戰來自于硬件和軟件兩個方面。對于軟件方面，挑戰集中于波形設計，信號處理和數據處理三個方面。通常雷達依據距離的探測應用需求分為近距離（SRR），中距離（MRR）和遠距離雷達（LRR）三種。在確定好應用需求之后，下一步便是確認可探測目標的距離，速度，角度的范圍和分辨率。針對這些要求需對波形進行定制化設計，同時這也最終將決定天線的設計和布局。

波形的設計包含：調制類型及參數，帶寬，信號發射和接收方法。波形不僅確定了處理接收信號采用何種算法，同時直接影響系統硬件的成本和復雜度。通常來說，雷達波形分為連續波和脈沖波。連續波一般需要分離的發射和接收天線。收發隔離的要求限制了發射功率，不過距離探測性能較好。另一方面對于脈沖信號，同一天線可以用于發射和接收，對功率要求有所降低，不過會導致距離盲區。在選擇波形時，適當的妥協是需要的。當然，在通信系統中，對于選定的波形，幅度、相位、頻率調制可以進一步應用其中。另外，極化的選擇也會對信號接收帶來較大的影響。

下面步入正題，本文將車載毫米波雷達領域最為常用的波形進行逐一的科普性介紹。

1.    連續波 - CW（Continuous Waveform）

波形如圖1所示。連續波有較好的多普勒分辨率（速度分辨），但不能解析距離。頻率分辨率為：

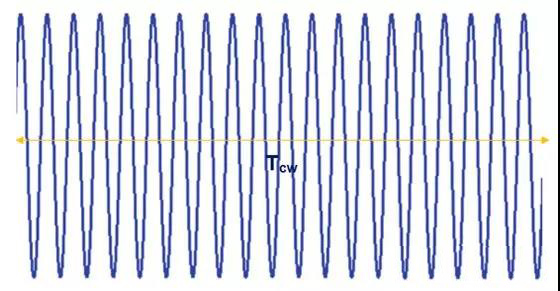
圖1. 連續波（CW）時域波形

2.    脈沖多普勒雷達波形 - Pulse DopplerRadar(PDR)

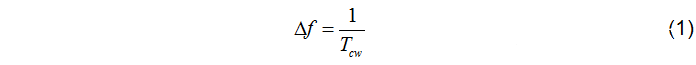
波形如圖2所示，脈沖多普勒雷達可以同時測量距離和速度，并具有較好的距離和速度分辨率。相應的距離和速度分辨為：

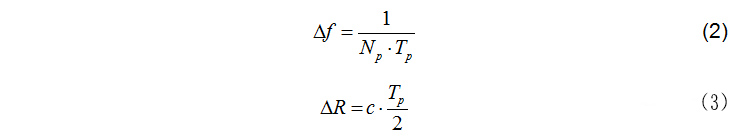
其中Tp為脈沖寬度，c為光速，Np為脈沖數量。

圖2.脈沖多普勒雷達時域波形

3.    頻率調制連續波 - Frequency-ModulatedCW (FMCW)

FMCW是車載毫米波雷達領域最為常用的波形。這種波形可以同時估計距離和速度，對硬件的要求相對低。上面提到的脈沖多普勒雷達可以實現相同的功能，不過對硬件的需求相對較高。FMCW的變種較多，下面逐一介紹。

3.1  線性頻率調制連續波 - linearfrequency-modulated CW (LFMCW)

如圖3所示，LFMCW體制雷達的頻率與時間呈線性關系，上掃頻和下掃頻構成對稱三角波形。發射信號和接收信號如圖3（a）所示，紅色線為發射信號，藍色線為目標的回波信號。圖3（b）為發射信號與回波信號的頻率差值信號，通常稱差頻或者差拍信號。

圖3. 線性頻率調制連續波時間頻率域波形

距離導致回波的時間延時，速度會引起多普勒頻移，收發信號混頻后獲得的差拍信號頻率由以下距離和速度引起的頻偏共同決定。

對于LFMCW上掃頻和下掃頻，滿足如下關系：

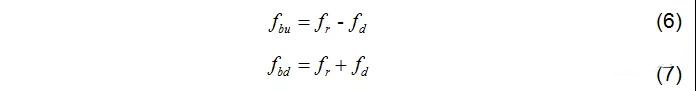
聯立(4)～(7)可得目標的距離和速度，如下所示。

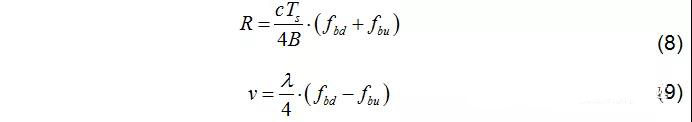
對于單目標場景，距離和速度可由上式無模糊的解析出來。對于多目標的情況，如何匹配同一目標的正負向差頻頻率是一個難點。配對模糊會導致本來不存在的目標被解析出來，導致鬼影（ghost）的產生。鬼影對于車載雷達來說是一個嚴重的問題，會導致對目標位置的錯誤判斷從而導致嚴重的問題。解決此問題需要結合其他的調制方式，比如可通過擴展其單個周期的波形序列的方法。如圖5所示，一個周期內的發射信號由兩段或更多不同斜率的信號組成，但這將增加系統的測量時間和算法的復雜程度。

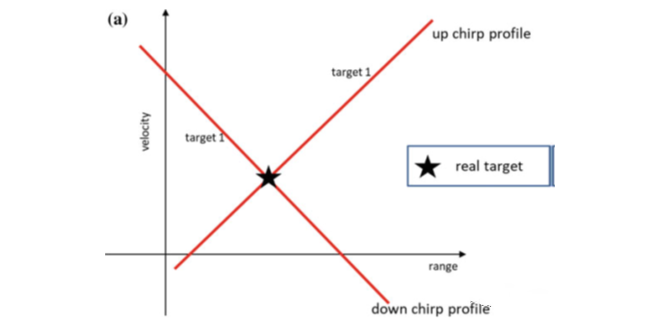
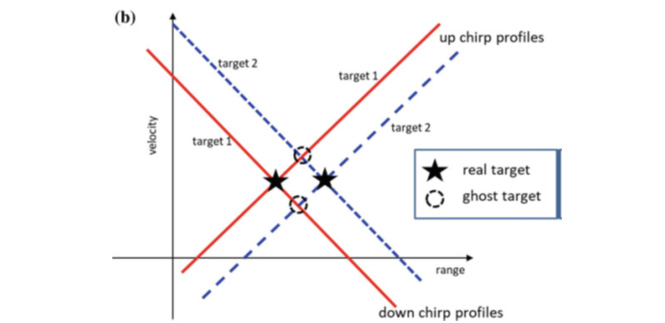
圖4.頻率配對模糊引起鬼影 (a) 單目標情況，距離和速度可以無模糊的解析； (b) 多目標情況，多個目標差頻信號的多個交點引起鬼影

圖5.多序列LFMCW波時間頻率域波形

3.2  步進FMCW波 - Stepped FMCW

波形如圖6所示，步進FMCW為一列頻率步進的階梯波形，每一階的頻率值恒定。此種波形特點是信號處理過程簡單，目標的距離信息可由相位信息獲得，對于距離R處的目標，采用兩階頻率為f1和f2波形， 響應的相位關系如下：

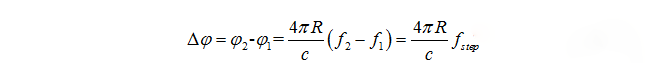
其中fstep表示步進頻率。可獲得目標距離：

最大模糊距離取決于fstep，以fstep = 5MHz為例，取相位最大2л。對應的最大可探測距離為：

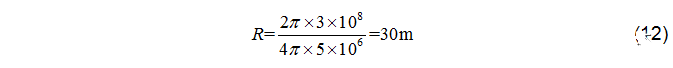
圖6. 多序列LFMCW波時間頻率域波形

3.3  多階頻移鍵控波形 - Multi-frequency Shift Keying (MFSK)，又名LFM+FSK波形

如圖6所示，兩組互相嵌入的步進序列A和B, A和B序列有固定的頻率偏移量。MFSK波形可以同時測量目標距離和速度信息，而不需進行頻率配對從而避免產生鬼影。基于A，B序列回波差頻信號的相位差值和跳頻可以計算目標距離：

其中，

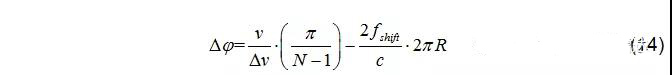
差拍信號頻率偏移由速度和距離共同引起，經FFT變換可得峰值點位置滿足：

聯立兩式可同時獲得速度和距離：

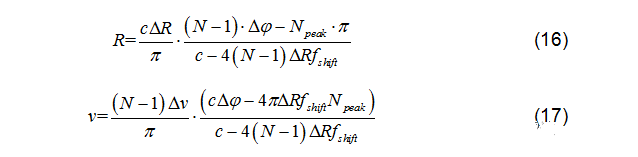
其中N表示傅里葉變換的采樣點數，由于每一階梯對應的差拍信號通常只采一個點，因此也等于A或B序列的階梯數。

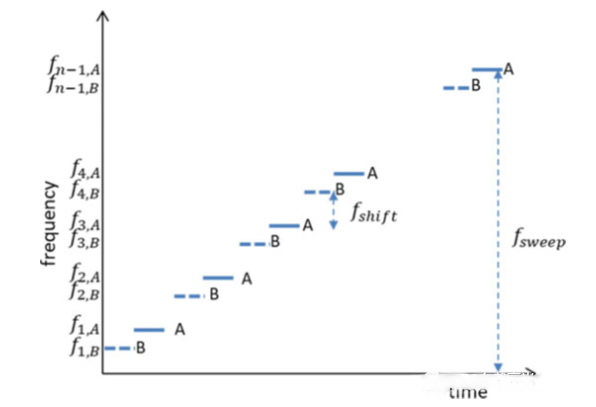
圖7.多階頻移鍵控時間頻率域波形

3.4  中斷FMCW波 - Interrupted FMCW (FMICW)

考慮收發隔離的問題，中斷FMCW波應運而生，如圖8所示。具體方式為分時的使能發射和接收通道，從而實現兩通道的隔離，解決互耦導致的近距離盲區，軍用雷達一般采用此種方式。

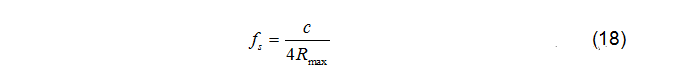
圖8.中斷FMCW波時間頻率域波形

如圖所示，對于靠近的目標，回波延時很小不易識別從而引起近距離目標盲區。對于遠距離處的目標，如果回波延時大于超出對應周期的接收時間會導致距離模糊。因此需在兩者間權衡。當目標的回波延時是發波開關周期的整數倍時，接收信號功率為零，導致距離盲區，為了避免此現象，開關時間頻率fs應該滿足條件。

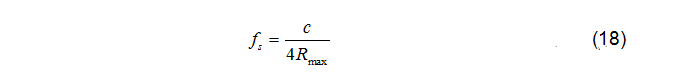
FMCIW波形在自動巡航（ACC）雷達中有一些應用。原因在于此類雷達通常采用FMCW波形，同時減少近距離雜波并增大最大探測距離很重要。

3.5  快掃序列 - Fast Chirp Ramp Sequence Waveform

如上所述，LFMCW波形在車載雷達中應用廣泛，但其主要的缺點在于多目標場景下，需要對每個目標的速度和距離進行正確配對從而避免鬼影。為了避免這個問題，當前主流的有兩種波形，一種是上面提到多階頻移鍵控波形，另一種則是快掃序列，如圖9所示。

圖9.快掃序列時間頻率域波形  

圖中一個單邊的上掃頻信號稱為一個Chirp，其重復周期Tp，一個周期（一幀）包含K個Chirp。差拍信號表示為：

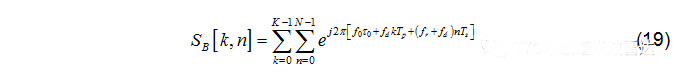
其中N為單個Chirp采樣點數，fd和fr分別為距離和速度引起的頻率偏移。對上式進行1D FFT （距離維 FFT），結果如下：

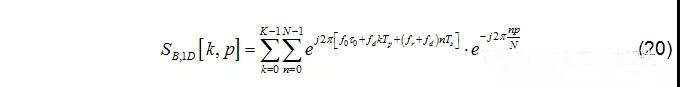
頻率峰值點位置：

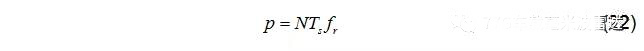
對上式進行2D FFT（多普勒維 FFT）：

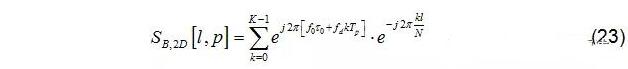
頻率峰值點位置：

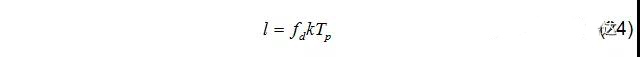
距離和速度的解析通過二維的FFT解析獲得。進一步的，通過對多個接收天線進行第三維的FFT可以獲得目標角度信息，如圖10所示。當然，對于目標角度的估計，方法和種類繁多，有更為專業的名字統稱波達角估計（Direction of Arrival）。舉例來說如24GHz雙天線體制，通常采用兩個接收天線進行相位減法后求得目標角度。對于77GHz頻段，通常采用的方法有FFT，DBF（數字波束形成），Capon波束形成，MUSIC（多重信號分類），ESPRIT（基于旋轉不變技術的信號參數估計）。前兩者為常規的物理分辨，提高角度分辨率的方法為增大天線口徑，或者等效的增加天線數量（MIMO）。后者為超分辨的方法，不過多的受限于天線數量。

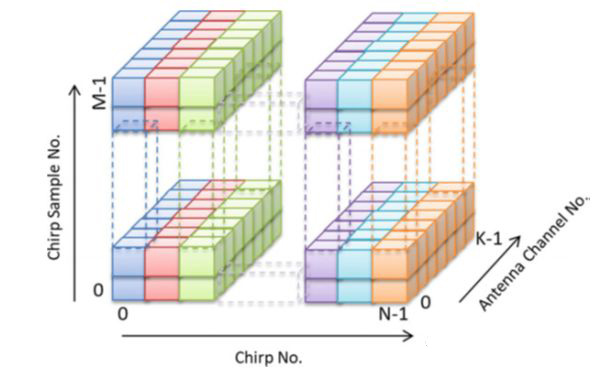
圖10.快掃序列3D數據矩陣

最后，需要指出在波形設計的過程中，會涉及到波形，天線配置，信號處理算法的多輪迭代直到其綜合滿足目標的探測應用需求。有時會是一比較耗時的過程。